Nuclear weapons can be made to have pretty much as much of a bang as one wants to make them, but with increased explosive yield comes an increased weapon weight. We always talk vaguely about being able to make H-bombs to arbitrarily high yields, but recently I’ve been mulling over this fact somewhat quantitatively. I gave a talk last month at the History of Science Society Meeting on US interest in 50-100 MT bombs around the time of the Limited Test Ban Treaty, and while working on this paper I got slightly obsessed with what is known as the yield-to-weight ratio.
Little Boy — a big bang compared to a conventional bomb, but still a very crude nuclear bomb.
What makes nuclear weapons impressive and terrible is that their default yield-to-weight ratio — that is, the amount of bang per mass, usually expressed in terms of kilotons per kilogram (kt/kg) — is much, much higher than conventional explosives. Take TNT for example. A ton of TNT weighs, well, a ton. By definition. So that’s 0.001 kilotons per 1,000 kilograms; or 0.000001 kt/kg. By comparison, even a crude weapon like the Little Boy bomb that was dropped on Hiroshima was about 15 kilotons in a 4,400 kg package: 0.003 kt/kg. That means that the Little Boy bomb had an energy density three orders of magnitude higher than a regular TNT bomb would. Now, TNT isn’t the be-all and end-all of conventional explosives, but no conventional explosive gets that much boom for its buck compared to a nuke.
The Little Boy yield is much lower than the hypothetical energy density of uranium-235. For every kilogram of uranium-235 that completely fissions, it releases about 17 kt/kg. That means that less than a kilogram of uranium-235 fissioned in the Little Boy bomb to release its 15 kilotons of energy. Knowing that there was 64 kg of uranium in the bomb, that means that something like 1.3% of the uranium in the weapon actually underwent fission. So right off the bat, one could intuit that this is something that could probably be improved upon.
Fat Man — a lot better use of fissile material than Little Boy, but no more efficient in terms of yield-to-weight.
The Fat Man bomb had a much better use of fissile material than Little Boy. Its yield wasn’t that much better (around 20 kilotons), but it managed to squeeze that (literally) out of only 6.2 kilograms of plutonium-239. Pu-239 releases around 19 kilotons per kilogram that completely fissions, so that means that around 15% of the Fat Man core (a little under 1 kg of plutonium) underwent fission. But the bomb itself still weighed 4,700 kg, making its yield-to-weight ratio a mere 0.004 kt/kg. Why, despite the improve efficiency and more advanced design of Fat Man, was the yield ratio almost identical to Little Boy? Because in order to get that 1 kg of fissioning, it required a very heavy apparatus. The explosive lenses weighed something like 2,400 kilograms just by themselves. The depleted uranium tamper that held the core together and reflected neutrons added another 120 kilograms. The aluminum sphere that held the whole apparatus together weighed 520 kilograms. The ballistic case (a necessary thing for any actual weapon!) weighed another 1,400 kg or so. All of these things were necessary to make the bomb either work, or be a droppable bomb.
So it’s unsurprising to learn that improving yield-to-weight ratios was a high order of business in the postwar nuclear program. Thermonuclear fusion ups the ante quite a bit. Lithium-deuteride (LiD), the most common and usable fusion fuel, yields 50 kilotons for every kilogram that undergoes fusion — so fusion is nearly 3 times more energetic per weight than fission. So the more fusion you add to a weapon, the better the yield-to-weight ratio, excepting for the fact that all fusion weapons require a fission primary and usually also have very heavy tampers.
I took all of the reported American nuclear weapon weights and yields from Carey Sublette’s always-useful website, put them into the statistical analysis program R, and created this semi-crazy-looking graph of American yield-to-weight ratios: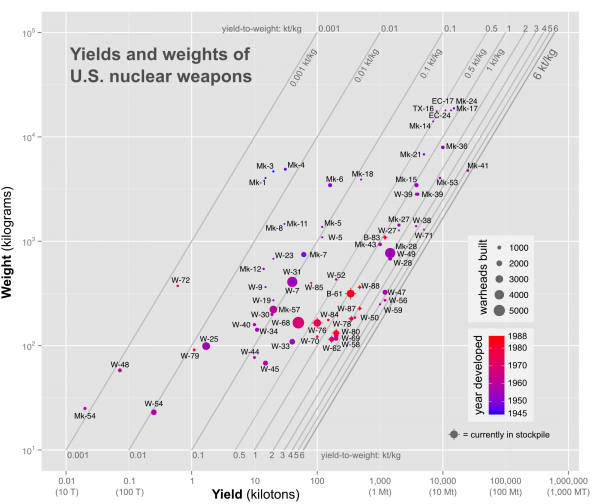
The horizontal (x) axis is the yield in kilotons (on a logarithmic scale), the vertical (y) axis is the weight in kilograms (also on a log scale). In choosing which of the weights and yields to use, I’ve always picked the lowest listed weights and the highest listed yields — because I’m interested in the optimal state of the art. The individual scatter points represent models of weapons. The size of each point represents how many of them were produced; the color of them represents when they were first deployed. Those with crosses over them are still in the stockpile. The diagonal lines indicate specific yield-to-weight ratio regions.
A few points of interest here. You can see Little Boy (Mk-1), Fat Man (Mk-3), and the postwar Fat Man improvements (Mk-4 — same weight, bigger yield) at the upper left, between 0.01 kt/kg and 0.001 kt/kg. This is a nice benchmark for fairly inefficient fission weapons. At upper right, you can see the cluster of the first H-bomb designs (TX-16, EC-17, Mk-17, EC-24, Mk-24) — high yield (hence far to the right), but very heavy (hence very high). Again, a good benchmark for first generation high-yield thermonuclear weapons.
What a chart like this lets you do, then, is start to think in a really visual and somewhat quantitative way about the sophistication of late nuclear weapon designs. You can see quite readily, for example, that radical reductions in weight, like the sort required to make small tactical nuclear weapons, generally results in a real decrease in efficiency. Those are the weapons in the lower left corner, pretty much the only weapons in the Little Boy/Fat Man efficiency range (or worse). One can also see that there are a few general trends in design development over time if one looks at how the colors trend.
First there is a movement down and to the right (less weight, more yield — improved fission bombs); there is also a movement sharply up and to the right (high weight, very high yield — thermonuclear weapons) which then moves down and to the left again (high yield, lower weight — improved thermonuclear weapons). There is also the splinter of low-weight, low-yield tactical weapons as well that jots off to the lower left. In the middle-right is what appears to be a sophisticated “sweet spot,” the place where all US weapons currently in the stockpile end up, in the 0.1-3 kt/kg range, especially the 2-3 kt/kg range: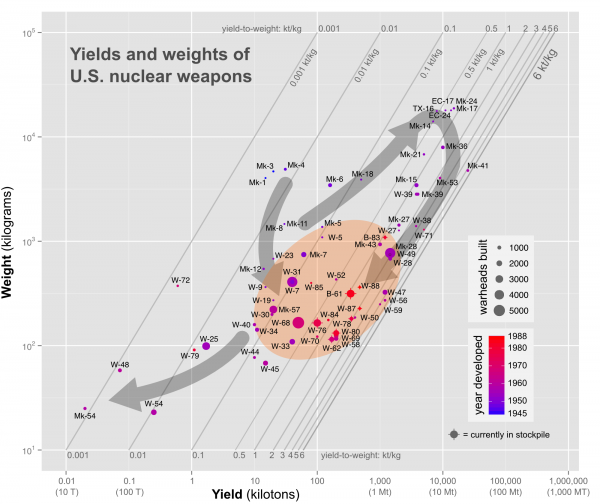
These are the bombs like the W-76 or the B-61 — bombs with “medium” yield warheads (100s rather than 1,000s of kilotons) in relatively low weight packages (100s rather than 1000s of kilograms). These are the weapons take advantage of the fact that they are expected to be relatively accurate (and thus don’t need to be in the multi-megaton range to have strategic implications), along with what are apparently sophisticated thermonuclear design tricks (like spherical secondaries) to squeeze a lot of energy out of what is a relatively small amount of material. Take the W-76 for example: its manages to get 100 kilotons of yield out of 164 kilograms. If we assume that it is a 50/50 fission to fusion ratio, that means that it manages to fully fission about 5 kilograms of fissionable material, and to fully fuse about 2 kilograms of fusionable material. And it takes just 157 kg of other apparatus (and unfissioned or unfused material) to produce that result — which is just a little more than Shaquille O’Neal weighs.
Such weapons aren’t the most efficient. Weapon designer Theodore Taylor wrote in 1987 that 6 kiloton/kilogram had been pretty much the upper limit of what had even been achieved.1 Only a handful of weapons got close to that. The most efficient weapon in the US stockpile was the Mk-41, a ridiculously high yield weapon (25 megatons) that made up for its weight with a lot of fusion energy.
The components of the B-61 nuclear weapon — the warhead is the bullet-shape in the mid-left. The B-61 was designed for flexibility, not miniaturization, but it’s still impressive that it could get 20X the Hiroshima bomb’s output out of that garbage-can sized warhead.
But given that high efficiency is tied to high yields — and relatively high weights — it’s clear that the innovations that allowed for the placing of warheads on MIRVed, submarine-launched platforms are still pretty impressive. The really magical range seems to be for weapons that in the hundred kiloton range (more than 100 kilotons but under a megaton), yet under 1,000 kilograms. Every one of those dates from after 1962, and probably involves the real breakthroughs in warhead design that were first used with the Operation Dominic test series (1962). This is the kind of strategic miniaturization that makes war planners happy.
What’s the payoff of thinking about these kinds of numbers? One is that it allows you to see where innovations have been made, even if you know nothing about how the weapon works. In other words, yield-to-weight ratios can provide a heuristic for making sense of nuclear design sophistication, comparing developments over time without caring about the guts of the weapon itself. It also allows you to make cross-national comparisons in the same fashion. The French nuclear arsenal apparently developed weapons in that same miniaturized yield-to-weight range of the United States by the 1970s — apparently with some help from the United States — and so we can probably assume that they know whatever the United States figured out about miniaturized H-bomb design in the 1960s.
The Tsar Bomba: a whole lot of boom, but a whole lot of weight. The US thought they could make the same amount of boom for half the weight.
Or, to take another tack, and returning to the initial impetus for me looking at this topic, we know that the famous “Tsar Bomba” of the Soviet Union weighed 27,000 kilograms and had a maximum yield of 100 Mt, giving it a yield-to-weight ratio of “only” 3.43 kilotons/kilograms. That’s pretty high, but not for a weapon that used so much fusion energy. It was clear to the Atomic Energy Commission that the Soviets had just scaled up a traditional H-bomb design and had not developed any new tricks. By contrast, the US was confident in 1961 that they could make a 100 Mt weapon that weighed around 13,600 kg (30,000 lb) — an impressive 7.35 kiloton/kilogram ratio, something well above the 6 kt/kg achieved maximum. By 1962, after the Dominic series, they thought they might be able to pull off 50 Mt in only a 4,500 kg (10,000 lb) package — a kind of ridiculous 11 kt/kg ratio. (In this estimate, they noted that the weapon might have an impractically large diameter as a result, perhaps because the secondary was spherical as opposed to cylindrical.) So we can see, without really knowing much about the US had in mind, that it was planning something very, very different from what the Soviets set off.
It’s this black box approach that I find so interesting about these ratios. It’s a crude tool, to be sure, but a tool nonetheless. By looking at the broad trends, we get insights into the specifics, and peel back the veil just a tiny bit.
Tags: 1940s, 1950s, 1960s, Bomb design, Graphic design, H-bomb, Nuclear testing
This entry was posted on Monday, December 23rd, 2013 at 9:20 am and is filed under Meditations. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.
Citation: Alex Wellerstein, “Kilotons per kilogram,” Restricted Data: A Nuclear History Blog, December 23, 2013, accessed July 7, 2024, https://blog.nuclearsecrecy.com/2013/12/23/kilotons-per-kilogram/.
I would just note that “according to the Soviet [intelligence] data, W76 has the weight of 91.7 kg (of which 61.5 kg was the nuclear charge, 22.7 kg – reentry vehicle body, and 6.7 kg – electronics)”. As you can see, RV body adds significant weight. But in the end, it doesn’t change the picture too much.
Interesting! There are some people (Chuck Hansen was one of them) who think that one should only judge the yield-to-weight ratio by the warhead itself, though I’m of the mindset that a bare warhead is probably not very useful, and that the total package matters. But as you note, even playing with the numbers a bit doesn’t generally change their overall location in the graph, since the physics package is so massive anyway and since it is a log scale.
This is really interesting stuff, Alex. It helps to answer one of the most elemental—but least frequently asked—questions one can ask about the history of science and technology: what were these people doing all this time, and what, to them, denoted quality or sophisticated work. I bet the story gets especially interesting when overlaid against the history of the designs of missiles and guidance systems, and the history of strategic problems such as the perceived need to destroy hardened targets. Then again, it’s possible that once the basic goal has been set—maximize the yield-to-weight ratio, or some such—bomb design could proceed independently of other developments. I certainly don’t know, and would be interested in your thoughts.
As you point out, this black-box approach doesn’t get us to the “tricks of the trade” that probably occupied many of the waking thoughts of bomb designers. But, in any case, this is really fine work in posing and answering kinds of questions that I don’t hear asked very often.
When they combined those “sweet spot” (100-300 kt or so) nukes with very accurate missiles, it lets them put a ridiculous amount of overpressure onto relatively small and specific areas. So that lets them do impressive things with hard targets, where previously they would need some multi-megaton weapon to compensate for their lack of accuracy. That’s my understanding, anyway. So this goes very much hand-and-hand with missile accuracy developments, I think.
Hear, hear. This stuff is fascinating. Somewhat related, I searched for ‘spherical secondaries’ based on something you mentioned in the article above. I was directed to a Wikipedia article on the W-88. As you can in the picture (http://en.wikipedia.org/wiki/File:W-88_warhead_detail.png) it shows a Uranium sparkplug as opposed to Plutonium. I was under the impression that Plutonium was more efficient than Uranium. Assuming the pic is accurate do you know why U would be used vs. Pu?
I don’t really know, Ben, but that’s an interesting question. I would presume that the situations you’d want U-235 instead of Pu-239 are when you need to minimize the background radiation level, or you want something with a slightly higher critical mass. Since the W-88 apparently uses a U-235 pusher on the secondary as well, maybe that’s just too much background activity to be safe?
I’m guessing that the energy yield of the Mark-41, our highest-yield bomb, was about 90% fission. The high yield-to-weight ratio was due to the very efficient use of fusion neutrons to cause fission in the tertiary stage, which, in addition to being unusually large, was held together by radiation implosion driven by the secondary stage. The tertiary stage of a three-stage bomb could approach 100% consumption of its fission and fusion fuel, but the result was a multi-megaton explosion that was too large to be of any practical use. I don’t know of any other U.S. bombs with more than two stages: the primary and the secondary. Apparently, the three-stage bomb, with its highly efficient tertiary, cannot be miniaturized.
Excellent point, Howard — this was my thinking as well. The fusion gets you a lot of boom-for-buck both because of its own inherent energy density being so high, but also because it allows for such efficient use of fissionable material.
Is there any indication that the U.S. used weapon weight as a way to control the devices? I could imagine anything over 100 kilos would be difficult for a single person to move, and thus much more difficult for a single person to squirrel away. Unless there was a reason why the bombs needed to be carried by a single person, higher weights could be a safety device, just as the separate launch switches in a Titan silo ensured that two people agreed that the missile should be launched.
That’s an interesting question. I doubt they ever added weight just as a security measure. Even the very light ones were still pretty heavy, and the priority seems to have always been on delivery, which usually meant on as little weight as possible. I would suspect that if the security question ever got reduced to just “could someone physically take this if they wanted to” that would be considered a significant security problem in and of itself.
The SADM used such a scheme, in my opinion. The lock secured cover was massive for such a stubby system.
in all the other systems, the military characteristics drove the weight to footprint equation.
Yeah, the only place I was thinking of this being a possibility was the SADM or Davy Crockett, but even then I figured that the fact that they were explicitly meant to be man-portable meant that you would want them to be, well, man-portable, and thus not weigh them down overly except perhaps while storing them.
My father, who was Army Special Forces and retired in 1981 when I was born after 21 years in, told me about doing ruck marches with a SADM between Ft. Bragg and Camp Mackall. To be honest, I kind of smiled and nodded, as my dad was an amazing story teller and I USED to think he was prone to artistic license. He passed away just after I graduated high school. As I’ve met friends of his and grown older, I’ve discovered he used artistic license far less than I thought. I remembered it as some form of a word like sadist, though not really believing the idea of a back-pack nuke. You can imagine my shock when I developed an intense fascination in high energy physics.
He did joke though, “I always thought that if I ever got sent to use the damned thing, once me and the team leader armed it, a little hatch would pop open with a little American flag popping out.. a fan would cause it to flutter in the breeze followed by a recoding of the star spangled banner and a recording saying, “We thank you for your service to your country… no don’t run, you’ve only got 4 seconds….”
For your “warheads built” data, are you using the most up-to-date figures here? – http://bos.sagepub.com/content/65/4/72.full.pdf+html. These supersede what’s in Atomic Audit and are also more recent than what can be found on Sublette’s pages.
I just used Carey’s data, in part because it was easy and in part because I don’t think the specifics of the numbers mattered too much, just the order of magnitudes.
And it takes just 157 lbs of other apparatus (and unfissioned or unfused material) to produce that result — less weight than the average American adult male.
You appear to have switched units from kg to lbs here without adjusting the number – unless the average American male is somewhat more overweight than I imagine, 157kg is probably closer to two of them.
You are correct, somehow I slipped a cog there. I’ve fixed the units and added another appropriate (?) comparison.
—Thought: all, or almost all of these, were assembly line, mass produced weapons, which thousands of ordinary air force workers would see in the course of their jobs.
—If someone ordered a “one of a kind, spare no expenses, different from all the others” nuclear explosive, can we guess what the yield to weight ratio would be?
—In the world of cars, two stretched convertibles with armored bodies were built in 1956 for the United States Secret Service. The brakes wore out frequently, and had to be replaced often, and since they were used for Presidential protection, the maintenance budget was probably closer to a jet fighter than a mass produced, assembly line car.
—Under those circumstances, what could we guess about nuclear weapons design?
Hi Bradley — The more fusion energy involved in the release, the better the yield-to-weight ratio gets. The more fission you add, the more you drive it down a bit. The more tampers and other heavy, non-reactive additions you need, the more you really drive it down.
So I don’t know what the theoretical maximum would be — presumably that would require a lot of knowledge about what tricks one would employ to get a lot of fusion without too many tampers.
One quickly gets into “probably not going to be deliverable by a rocket or plane” territory when one starts to imagine even very favorable ratios for gigaton-range weapons. Which doesn’t rule out their development or delivery, of course, but does make them unappealing to, say, the Air Force. And the utility of such a weapon is, of course, not very high when compared to the utility of having many, easy-to-deliver, medium-sized nukes. There was, as I mentioned, some US interest in the question of how big they could practically make a bomb, and they concluded that even very-advanced, very-efficient 100 Mt weapons involved weights and diameters that made them extremely undesirable.
[…] One of the most interesting documents I found in an online database — an estimate for the ease of developing a 100 megaton weapon in a letter from Glenn Seaborg to Robert McNamara. Knowing the estimated yield and weight of the bombs in question allows one to divine a lot of inform…. […]
> The explosive lenses weighed something like 2,400 kilograms just by themselves. The depleted uranium tamper that held the core together and reflected neutrons added another 120 kilograms. The aluminum sphere that held the whole apparatus together weighed 520 kilograms. The ballistic case (a necessary thing for any actual weapon!) weighed another 1,400 kg or so. All of these things were necessary to make the bomb either work, or be a droppable bomb.
(2400 + 120 + 520 = 3040 кг)
Сферический заряд РДС-1 весил 2900 кг (“Атомный проект СССР” т.2, кн.7, с 220).
> … we know that the famous “Tsar Bomba” of the Soviet Union weighed 27,000 kilograms and had a maximum yield of 100 Mt, …
Явный прогресс.
За 5 лет до этого считалось, что масса боеприпаса мощностью в 150 Мт будет составлять 100 т (при использовании, в основном, природного лития, – 500 т). Там же – об изделии на 1 Гт:
”
Записка А.Д. Сахарова, Я.Б. Зельдовича и В.А. Давиденко Н.И. Павлову с оценкой параметров изделий мощностью в 150 мегатонн и один миллиард тонн ТНТ 2 февраля 1956 г.
Товарищу Павлову Н.И.
Сообщаем оценку параметров изделия мощностью в 150 мегатонн ТНТ.
I вариант Изделие с дейтеридом лития (…)%[-ого] обогащения, по-видимому, может быть сделано в следующих габаритах:
1) диаметр 4 метра,
2) длина — 8–10 метров,
3) общий вес — около 100 тонн.
При этом потребуются активные материалы в количествах:
1) U 235 — около (…) кг,
2) дейтерида лития-6 — около (…) тонн,
3) природного урана (можно обедненного) — около (…) тонн.
II вариант Изделие с уменьшенным расходом лития-6 и с использованием природного лития может быть сделано в габаритах:
1) диаметр — 6 -7 метров,
2) длина — 18–20 метров,
3) общий вес — около 500 тонн.
Активных материалов потребуется:
1) U 235 — около (…) кг,
2) дейтерида лития-6 — около (…) тонн,
3) дейтерида природного лития — около (…) тонн,
4) естественного урана (можно обедненного) — около (…) тонн.
Изделие мощностью в один миллиард тонн ТНТ может быть изготовлено по любому из этих двух вариантов при увеличении весов дейтеридов и природного урана в 6-7 раз, а весов делящихся материалов — приблизительно в 3 раза.
”
http://www.iss-atom.ru/pub/pub-156.htm
[…] yields a thousand times more powerful than the Hiroshima bomb, but that you could make them in small-enough packages that they could fit onto airplanes. It is was what truly inaugurated the megaton age (more so than […]
Enter your email address to subscribe to this blog and receive notifications of new posts by email. You can unsubscribe anytime.
All text copyright (©) 2011-2024 by Alex Wellerstein, unless otherwise specified.